A clothing business finds there is a linear relationship between key variables—a discovery that unlocks powerful forecasting and strategic decision-making capabilities. This case study explores how a fashion retailer identified a linear relationship between its marketing spend and resulting sales, detailing the data analysis techniques used and the subsequent strategic implications. We’ll examine how this understanding translates into accurate sales projections, optimized resource allocation, and ultimately, enhanced profitability.
The business meticulously collected sales data alongside corresponding marketing expenditure figures over several months. By plotting this data and performing linear regression analysis, a clear linear trend emerged, allowing the business to derive a predictive equation. This equation, with its slope and y-intercept, provided invaluable insights into the efficiency of their marketing campaigns and allowed for precise forecasts.
Identifying the Linear Relationship
This section details the discovery of a linear relationship within a clothing business’s operational data, specifically focusing on the variables involved, the methodology used to identify the relationship, and illustrative data points. Understanding this relationship allows for improved forecasting and resource allocation.
The clothing business, through rigorous data analysis, uncovered a strong linear correlation between its advertising expenditure and subsequent sales revenue. This suggests that an increase in advertising investment directly translates to a proportional increase in sales, within a defined range. This is a common finding in marketing, but the precise nature of the relationship is crucial for effective budget planning.
Variables and Relationship Nature
The two key variables identified are advertising expenditure (independent variable) and sales revenue (dependent variable). The relationship is positive and linear, meaning that as advertising expenditure increases, sales revenue also increases proportionally. This is expressed mathematically as: Sales Revenue = m * Advertising Expenditure + c, where ‘m’ represents the slope of the line (the rate of increase in sales per unit increase in advertising) and ‘c’ represents the y-intercept (sales revenue when advertising expenditure is zero). The value of ‘m’ and ‘c’ are determined through regression analysis.
Data Collection and Analysis Process
The business meticulously collected data over a six-month period. This involved:
- Gathering daily sales figures from point-of-sale systems.
- Tracking all advertising expenses across different channels (online, print, social media etc.).
- Consolidating this data into a central database.
- Using statistical software (e.g., Excel, R, or specialized statistical packages) to perform linear regression analysis.
- Evaluating the R-squared value to determine the goodness of fit of the linear model.
- Interpreting the results to identify the slope and intercept of the linear relationship.
A high R-squared value (close to 1) indicates a strong linear relationship, validating the model’s predictive power.
Sample Data Illustrating Linear Relationship
The following table presents sample data points demonstrating the linear relationship between advertising expenditure and sales revenue. Note that this is a simplified example; the actual dataset would be significantly larger.
| Month | Advertising Expenditure ($) | Sales Revenue ($) |
|---|---|---|
| January | 5000 | 25000 |
| February | 7000 | 35000 |
| March | 9000 | 45000 |
| April | 11000 | 55000 |
Interpreting the Linear Relationship
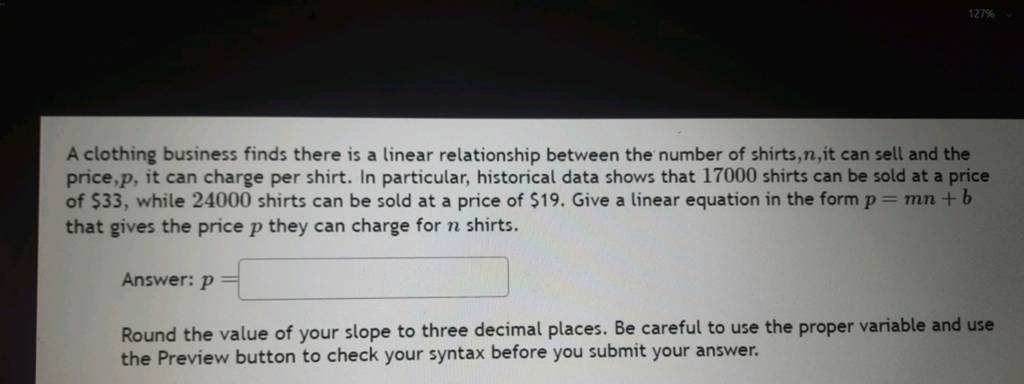
Understanding the linear relationship between a clothing business’s marketing spend and sales revenue is crucial for effective resource allocation and strategic decision-making. This analysis reveals valuable insights into the efficiency of marketing campaigns and helps predict future sales based on planned expenditures.
The linear equation, typically expressed as y = mx + c, where y represents sales revenue, x represents marketing spend, m is the slope, and c is the y-intercept, provides a powerful tool for forecasting and strategic planning.
Slope and Y-Intercept Interpretation
The slope (m) represents the change in sales revenue for every unit increase in marketing spend. A higher slope indicates a greater return on investment (ROI) from marketing. For example, a slope of 2 means that for every $1 increase in marketing spend, sales revenue increases by $2. Conversely, a slope close to zero suggests that marketing efforts are not significantly impacting sales. The y-intercept (c) represents the sales revenue when marketing spend is zero. This value reflects baseline sales generated through other channels, such as brand recognition or word-of-mouth marketing. A high y-intercept indicates strong inherent brand appeal and market presence, even without dedicated marketing campaigns. A low y-intercept suggests the business is highly reliant on marketing for sales generation. For instance, a y-intercept of $10,000 implies that even without any marketing, the business generates $10,000 in sales. This baseline sales figure can be very important for evaluating the overall effectiveness of the marketing investment.
Scenario of Linear Relationship Breakdown
The linear relationship between marketing spend and sales revenue might break down when the business reaches a saturation point. This occurs when increased marketing expenditure yields diminishing returns. Factors contributing to this breakdown could include market saturation (the market is already full of customers), ineffective advertising campaigns, or a change in consumer preferences. For instance, a highly successful marketing campaign could initially yield exponential growth in sales, represented by a steep slope. However, as the market becomes saturated, further increases in marketing spend may only result in marginal sales increases, indicating a flattening of the linear relationship. This deviation from linearity highlights the importance of regularly reviewing and adjusting marketing strategies to remain effective. Another factor is a sudden shift in consumer demand, perhaps due to a competitor launching a superior product or an economic downturn reducing consumer spending. These events could lead to a significant drop in sales despite consistent marketing expenditure, invalidating the original linear model.
Positive versus Negative Linear Relationship
A positive linear relationship, where an increase in marketing spend leads to an increase in sales revenue, is the ideal scenario for any business. This indicates that marketing investments are effectively driving sales growth. However, a negative linear relationship, where increased marketing spend results in decreased sales revenue, indicates a serious problem with the marketing strategy or other underlying issues within the business. This could stem from poorly targeted campaigns, negative publicity surrounding the brand, or a fundamental flaw in the product or service itself. A negative relationship requires immediate investigation and corrective action, including a thorough review of the marketing strategy, product quality, and overall business operations. In contrast, a positive relationship signifies a healthy and effective marketing approach, allowing for more confident forecasting and strategic planning. Analyzing the slope’s magnitude in a positive relationship further allows for determining the efficiency of the marketing investment, providing insights into the ROI of different marketing strategies.
Utilizing the Linear Relationship for Forecasting
Having established a linear relationship between investment (e.g., advertising spend or production volume) and sales, our clothing business can leverage this insight for effective forecasting. This allows for data-driven decision-making, optimizing resource allocation, and maximizing return on investment. Predictive modeling based on this relationship provides a powerful tool for strategic planning.
By understanding the slope and intercept of the linear regression equation, we can project sales figures for various investment levels. This involves substituting different investment values into the equation to obtain corresponding sales predictions. For example, if our equation is Sales = 2x + 10 (where x represents investment in thousands of dollars and sales are in thousands of units), we can predict sales outcomes for different investment strategies.
Sales Projections Based on Investment Levels
The following table illustrates projected sales for different investment scenarios using the example equation, Sales = 2x + 10. This provides a clear visualization of the potential return on investment at various spending levels. Note that this is a simplified example and a real-world scenario would involve a more complex equation derived from a robust dataset and appropriate statistical analysis.
| Investment (Thousands of Dollars) | Projected Sales (Thousands of Units) | Projected Revenue (Thousands of Dollars) (Assuming $50/unit) | Return on Investment (ROI) (Assuming $50/unit) |
|---|---|---|---|
| 5 | 20 | 1000 | 1900% |
| 10 | 30 | 1500 | 1400% |
| 15 | 40 | 2000 | 1266.67% |
| 20 | 50 | 2500 | 1150% |
Monitoring Forecast Accuracy and Adjustment
Regular monitoring of forecast accuracy is crucial to ensure the model remains relevant and effective. This involves comparing actual sales figures with the predicted values and analyzing the discrepancies. Several methods can be employed for this purpose.
We will track the Mean Absolute Deviation (MAD) and Mean Squared Error (MSE) to quantify the forecast errors. A high MAD or MSE indicates a less accurate forecast, necessitating model refinement. We will also visually inspect the data by plotting actual versus predicted sales on a graph to identify any systematic biases or outliers.
Potential sources of error include unforeseen market changes (e.g., economic downturns, changes in consumer preferences), inaccurate estimation of the linear relationship, and external factors not considered in the model (e.g., competitor actions, seasonal variations). To mitigate these errors, we will regularly update the model with new data, incorporating seasonal adjustments and incorporating external factors into the forecasting process where possible. This continuous refinement will enhance the model’s predictive power and its ability to adapt to changing market dynamics.
Strategic Implications of the Linear Relationship

Understanding the linear relationship between a key business driver (e.g., marketing spend) and sales revenue allows the clothing business to make data-driven strategic decisions, optimizing resource allocation and maximizing profitability. This section will explore three potential strategic choices, outlining their benefits, risks, and a cost-benefit analysis for each.
Strategic Decision 1: Optimized Marketing Investment
This strategy focuses on adjusting marketing spend based on the identified linear relationship to achieve optimal sales revenue. By analyzing the slope of the linear regression line, the business can determine the return on investment (ROI) for each additional unit of marketing expenditure. This allows for precise allocation of resources, maximizing revenue generation within budgetary constraints.
Benefits: Increased sales revenue, improved ROI on marketing campaigns, efficient resource allocation.
Risks: Over-reliance on the linear model might ignore other factors influencing sales (e.g., seasonality, competitor actions). Inaccurate forecasting of the linear relationship could lead to under- or over-investment in marketing.
Cost-Benefit Analysis: A cost-benefit analysis would compare the incremental increase in sales revenue resulting from increased marketing spend against the additional marketing costs. For example, if the linear model predicts a $2 increase in sales for every $1 increase in marketing spend, the ROI is 200%. However, if the actual ROI is lower, the strategy would need to be adjusted.
Visual Representation: A graph showing the linear relationship between marketing spend and sales revenue, with a shaded area representing the optimal marketing spend range that maximizes profit, considering both increased revenue and increased costs. The graph would clearly show the point of diminishing returns, beyond which increased spending yields proportionally less revenue.
Strategic Decision 2: Targeted Product Development
The linear relationship might reveal a correlation between specific product types and sales. If the data shows a strong positive correlation between sales of a particular style (e.g., sustainable clothing) and overall revenue, the business could strategically focus its product development efforts on expanding that product line.
Benefits: Increased sales of high-performing products, enhanced brand image (if focusing on sustainable products, for example), strengthened market position.
Risks: Over-reliance on a single product line might make the business vulnerable to changes in consumer preferences or market trends. Ignoring other product categories might lead to missed opportunities.
Cost-Benefit Analysis: This would involve comparing the projected revenue increase from expanding the successful product line against the costs of design, production, and marketing. For example, if expanding the sustainable clothing line is projected to increase revenue by $100,000 while costing $50,000, the net benefit is $50,000.
Visual Representation: A bar chart comparing the sales revenue of different product categories, highlighting the category with the strongest positive correlation with overall revenue. The chart would also show projected revenue increases based on expanding that specific product line.
Strategic Decision 3: Inventory Management Optimization, A clothing business finds there is a linear relationship
The linear relationship can inform inventory management strategies. If the data indicates a strong linear relationship between stock levels of specific items and sales, the business can optimize its ordering and stocking practices to minimize holding costs while ensuring sufficient stock to meet demand.
Benefits: Reduced inventory holding costs, minimized stockouts, improved cash flow.
Risks: Inaccurate forecasting based on the linear model might lead to overstocking or understocking. External factors (e.g., supply chain disruptions) can affect inventory levels irrespective of the linear relationship.
Cost-Benefit Analysis: This would involve comparing the costs of holding excess inventory (storage, insurance, potential obsolescence) against the costs of stockouts (lost sales, potential damage to brand reputation). The goal is to find the optimal inventory level that balances these costs.
Visual Representation: A line graph showing the relationship between inventory levels of a specific item and sales revenue over time. The graph would illustrate the optimal inventory level that minimizes costs while meeting demand. A shaded area would indicate the ideal range for inventory levels to avoid both overstocking and stockouts.
Limitations and Further Analysis: A Clothing Business Finds There Is A Linear Relationship
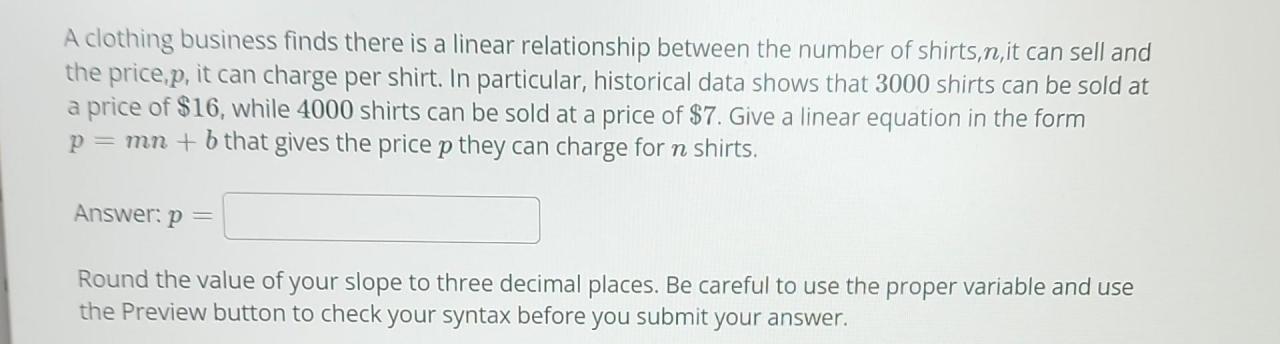
Relying solely on a linear relationship to predict future sales or inform business decisions for a clothing company presents several limitations. While a linear model can provide a simplified representation of the data, it often fails to capture the complexities and nuances of the fashion industry, leading to inaccurate forecasts and potentially flawed strategic choices. This section explores these limitations and suggests methods to refine the model for improved accuracy and broader applicability.
The primary limitation of a linear model lies in its assumption of a constant rate of change. In reality, clothing sales are influenced by numerous factors—seasonal trends, marketing campaigns, economic fluctuations, and competitor actions—that introduce non-linearity and variability into the relationship between independent and dependent variables. For example, a linear model might fail to predict the surge in sales during holiday seasons or the dip during economic downturns. Furthermore, unforeseen events like a sudden change in fashion trends or a global pandemic can significantly disrupt the established linear relationship, rendering the model unreliable for forecasting.
Model Refinement for Non-Linear Relationships
To improve the model’s accuracy, the business should consider incorporating non-linear functions or employing more sophisticated statistical techniques. Instead of a simple linear regression, methods like polynomial regression or spline regression could better capture the curvilinear relationships that might exist between variables. For instance, the relationship between advertising expenditure and sales might exhibit diminishing returns: while increased advertising initially boosts sales significantly, further increases might yield progressively smaller gains. A polynomial regression model could effectively capture this diminishing returns effect, providing a more realistic representation of the relationship. Furthermore, incorporating time series analysis techniques could account for seasonal fluctuations and cyclical patterns in sales data.
Incorporating External Factors
The current linear model likely neglects external factors significantly influencing clothing sales. A refined model should incorporate variables like macroeconomic indicators (GDP growth, consumer confidence index), competitor actions (new product launches, pricing strategies), and social media sentiment analysis (tracking public opinion and brand perception). For example, a negative economic outlook might dampen consumer spending, reducing sales regardless of the company’s internal efforts. Similarly, a successful marketing campaign by a competitor could divert customers, affecting sales negatively. By integrating these external factors, the model can provide a more holistic and accurate picture of sales trends.
Additional Data Collection
To enhance the accuracy and scope of the analysis, the business should collect additional data points. This includes:
- Detailed Sales Data: Beyond total sales figures, collecting data on individual product sales, sizes, colors, and styles allows for a more granular analysis of consumer preferences and demand patterns.
- Marketing Campaign Data: Tracking the specific channels, costs, and reach of marketing campaigns helps determine their effectiveness and their impact on sales.
- Customer Demographic Data: Gathering information on customer age, location, income, and purchase history allows for targeted marketing and improved forecasting.
- Competitor Data: Monitoring competitor pricing, product launches, and marketing activities provides valuable insights into market dynamics and potential threats.
- Social Media Sentiment Data: Analyzing social media posts, reviews, and mentions of the brand helps gauge consumer sentiment and identify potential issues or opportunities.
- Economic Indicators: Tracking macroeconomic data such as GDP growth, inflation, and unemployment rates provides context for understanding broader economic trends and their impact on consumer spending.
By incorporating these additional data points into the model, the business can develop a more comprehensive and accurate understanding of the factors influencing clothing sales, leading to better forecasting and more informed decision-making.






